拓扑排序 / topological sort

2017-11-22

2.1k words

问题描述: 提供一些以数字为 id 的任务(task)，这些任务存在如下图所示的依赖关系:

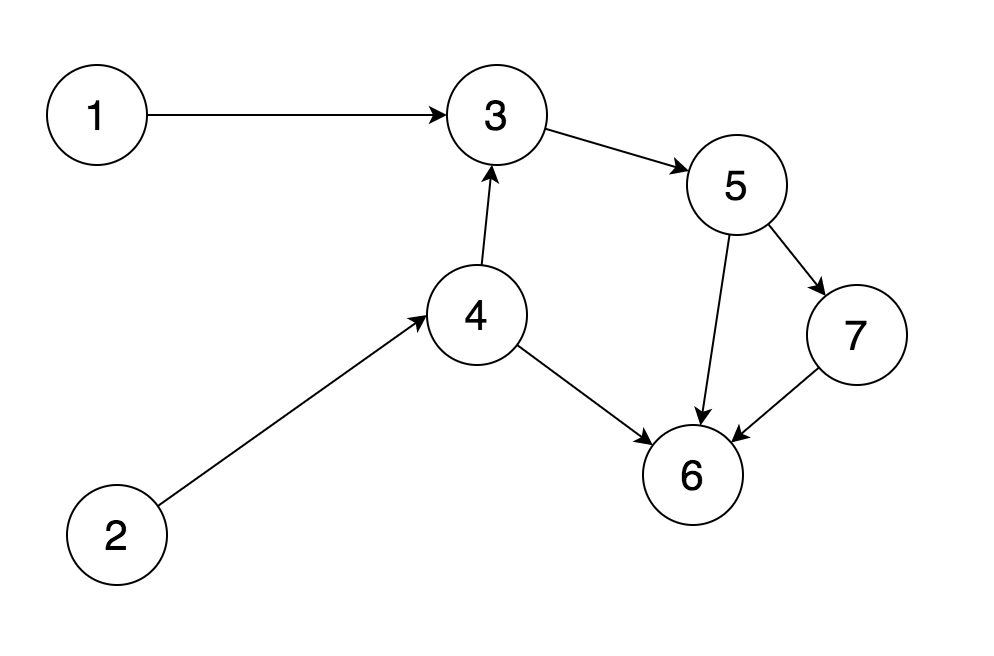
其中, 1 -> 3 表示任务 3 必须在任务 1 完成之后才能够开始。如上图中，任务 3 必须在任务 1 和任务 4 之后。而任务 4 又必须在任务 2 之后。

而要求就是, 提供一个序列，要求按照这个序列能够顺利完成所有任务。这里假设每个时刻只能处理一个任务，而且一旦开始处理某个任务，那么你不能中止或切换到其它任务。这个答案可能不唯一。在上图中，一个可能的答案就是 [1, 2, 4, 3, 5, 7, 6]。

算法描述

一个显然可以得到的观点就是，对于没有依赖的任务，可以直接将其放入所求的序列中，比如上图中的 [1, 2]。

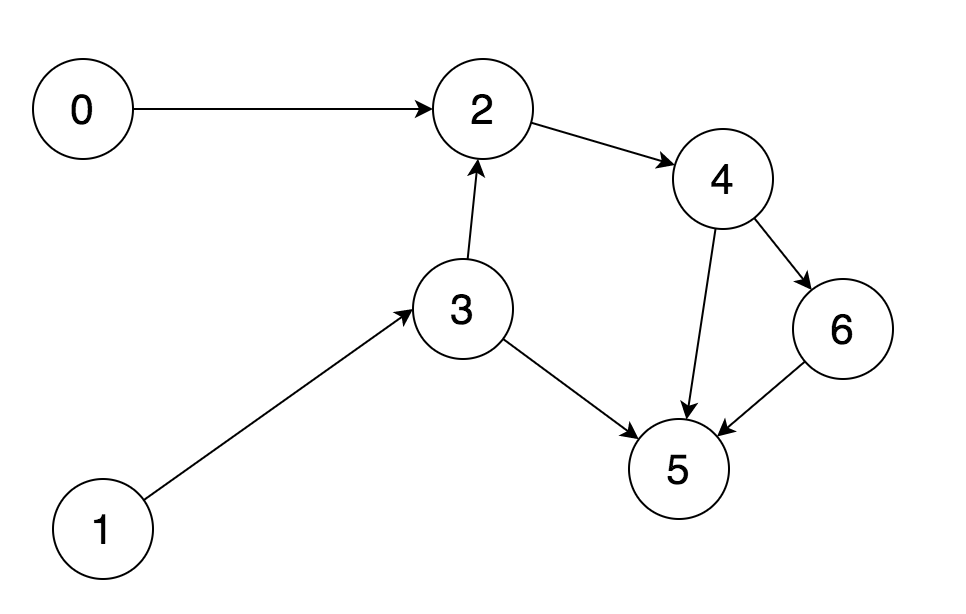
那算法的第一步就是找出所有没有被依赖的任务，并将其移除，此时可以得到一个新的图:

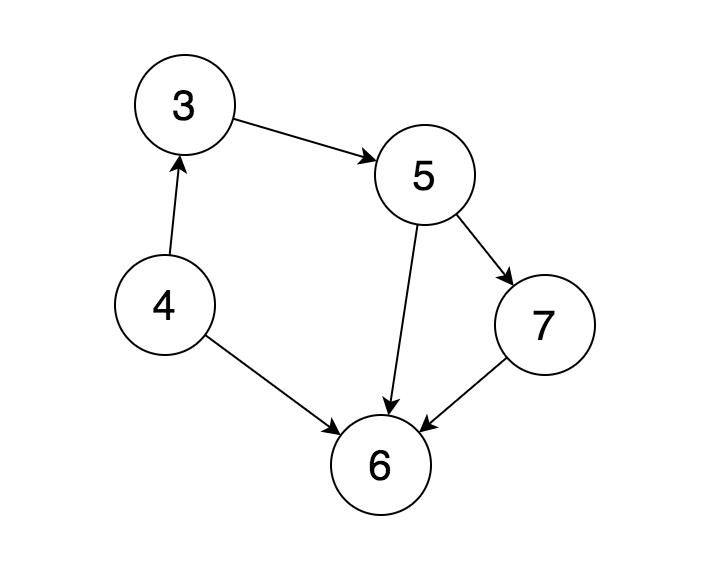
显然又可以发现，又出现了没有依赖的任务 [4]，那我们继续把它放入所求的序列中，并将其移除，得到的新的图:

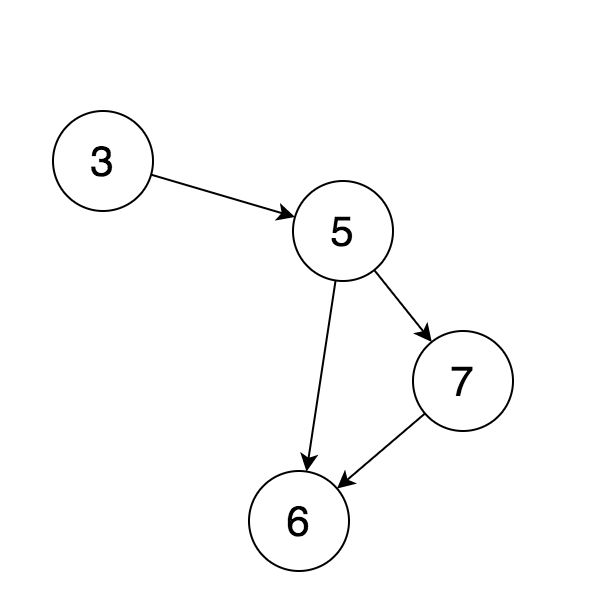
此时又得到新的图，而且同样出现了没有依赖的任务，所以继续把它放入序列中，将其移除。。。以此类推，每次移除没有依赖的点，得到新的图，继续移除没有依赖的点，直到所有的点都被移除了。

我们首先需要用一种数据结构表示一点任务是否有依赖。那我们可以发现，用依赖的数量来表示是否有依赖非常合适。如最开始的图中:

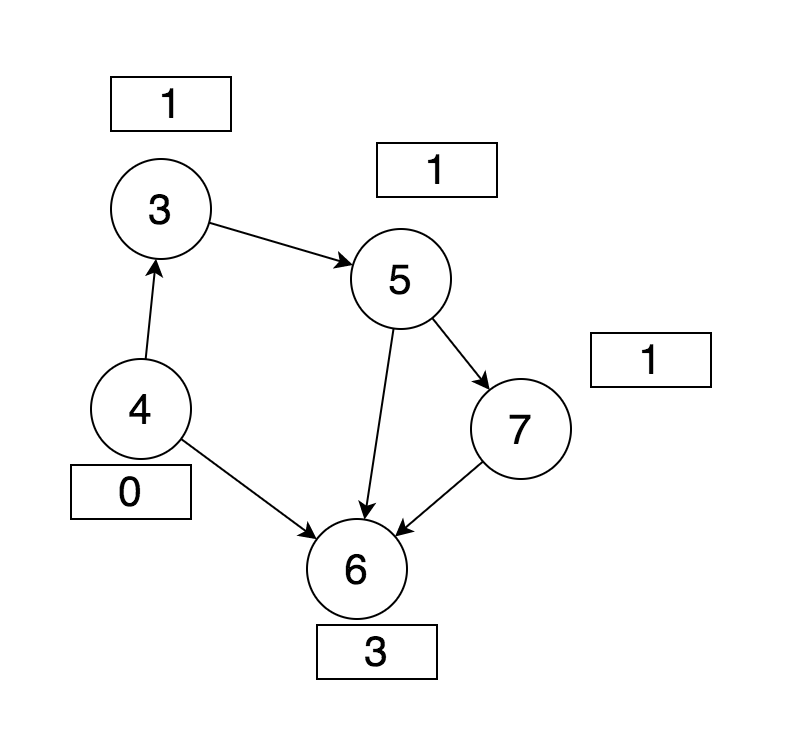
方块中的数字即表示旁边的任务的依赖数，如果数字为 0 即表示依赖为 0。而当我们把[1, 2] 移除后，相连的 [3, 4] 的依赖数必定会减少，变成如图所示:

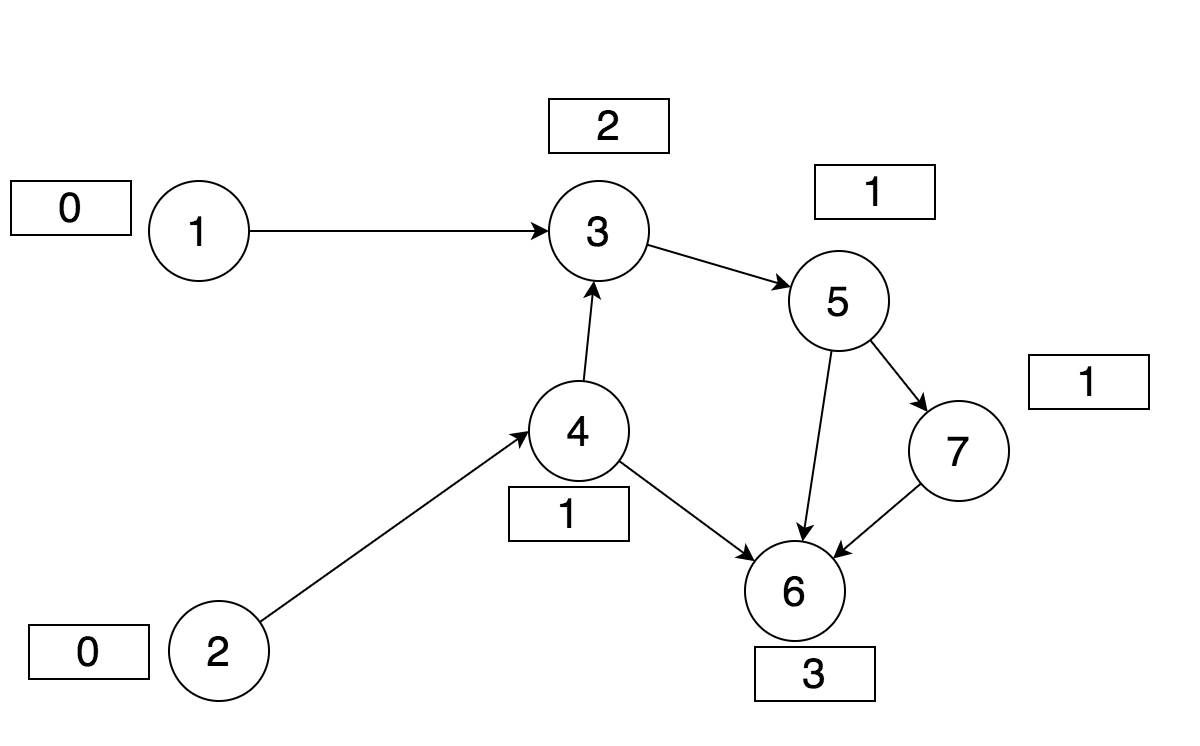
此时任务 4 的依赖数为 0，将其移除后，任务 3 的依赖数变为 0，任务 6 的依赖变为 2。所有下一次又移除 3。

而实际上，这里的依赖数有一个更专业的名词叫 入度。如其字面意思一样，对于某个点，有多少箭头指向它。

主流的实现方法有两种，BFS 和 DFS 。因为我更喜欢 BFS，所以这里用 BFS 解释。其中 Queue 的实现可以参照这里。

/**
 * numTasks 表示任务的数量，这里假设任务的 id 从 0 ~ numTasks
 *
 * prerequisites 是一个二维数组
 * 例如 [[3, 1], [4, 2], [3, 4]] 表示:
 * 任务 3 必须在任务 1 之后，任务 4 必须在任务 2 之后，任务 3 必须在任务 4 之后
 * 换言之，1 指向 3，2 指向 4，4 指向 1
 */
function topo (numTasks, prerequisites) {
  const indegrees = new Array(numTasks).fill(0) // 入度

  const links = Array.from({ length: numTasks }).map(_ => [])
  // 用一个二维数组表示图
  // 比如数组 links[5] = [6, 7] 表示 5 指向 6 与 7

  prerequisites.forEach(([second, first]) => {
    indegrees[second]++
    links[first].push(second)
  })

  const q = new Queue()
  const ans = []
  // 寻找 入度 为 0 的点
  ;[...Array(numTasks).keys()].filter(i => !indegrees[i]).forEach(x => q.push(x))
  while (!q.empty()) {
    const top = q.pop()
    ans.push(top)
    // 移除这个点的对应的边，所以相连的任务的入度都减一
    links[top].forEach(x => indegrees[x]--)
    // 入度减小的这些任务中是否有入度为 0 的点
    links[top].filter(x => !indegrees[x]).forEach(x => q.push(x))
  }
  return ans

对于此图的运行结果:

1 2	> topo(7, [[2, 0], [3, 1], [2, 3], [4, 2], [5, 3], [5, 4], [6, 4], [5, 6]]) [ 0, 1, 3, 2, 4, 6, 5 ]

复杂度

假设顶点数为 V，边的数目为 E，时间复杂度上讲，应该为 O(V + E)。

因为每一个点仅仅被访问一次，而每条边也都会被移除一次。

存在环

如果存在环，那么在某个时刻存在入度不为 0 的点，如下图所示:

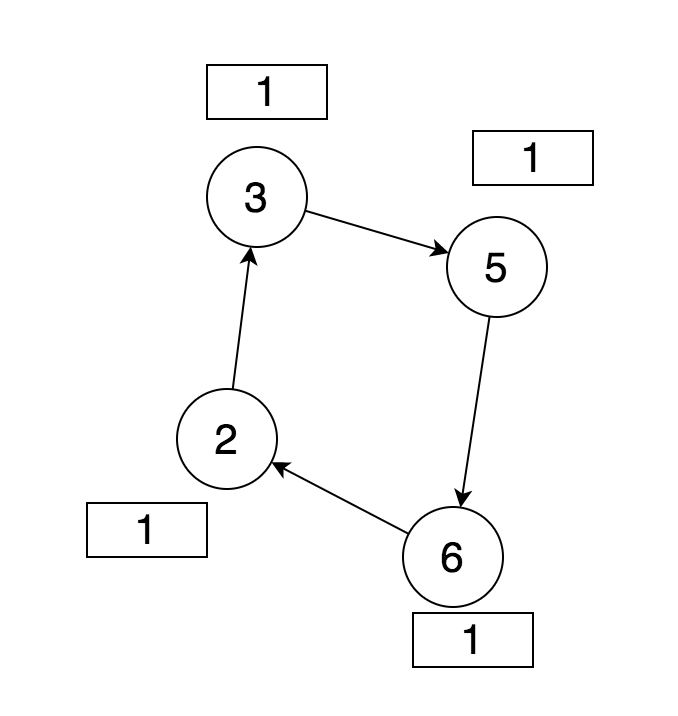
这种情况下，一般需要判断最后的序列长度是否为 numTasks。如果不是，则存在环。所以，这个算法也可以用于判断环的存在与否。

特别注意的是，即使存在环，上述代码中 while (!q.empty()) 也不会陷入死循环，原因是 q 包含的是入度为 0 的点，如果不存在了入度为 0 的点，那么就会终止循环。

例题

最后再说几句

最初这题是一位 FaceBook 的学长给我做 mock interview 出的题目。当时我知道这是拓扑排序，但没想到的是，我因为长期没有做这类题，已经完全忘记了它的具体做法。在当时的情况下，我并没有想起来怎么去做这题。所以说，平时偶尔还是要刷一些已经刷过的题呀。

参考

Wiki Topological Sorting

Categories

算法描述

复杂度

存在环

例题

最后再说几句

参考